The Size Effect Has a Lottery-Style Payoff
A new research paper related mainly to:
#25 – SIze Premium
Authors: McGee, Olmo
Title: The Size Premium As a Lottery
Link: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3279645
Abstract:
We investigate empirically the dependence of the size effect on the top performing stocks in a cross-section of risky assets separated by industry. We propose a test for a lottery-style factor payoff based on a stochastic utility model for an under-diversified investor. The associated conditional logit model is used to rank different investment portfolios based on size and we assess the robustness of the ranking to the inclusion/exclusion of the best performing stocks in the cross-section. Our results show that the size effect has a lottery-style payoff and is spurious for most industries once we remove the single best returning stock in an industry from the sample each month. Analysis in an asset pricing framework shows that standard asset pricing models fail to correctly specify the size premium on risky assets when industry winners are excluded from the construction of the size factor. Our findings have implications for stock picking, investment management and risk factor analysis.
Notable quotations from the academic research paper:
” Firms with small market capitalization tend to outperform larger companies. Investors are attracted to lottery-like assets with positively skewed returns because they o�ffer a very large payoff� with a small probability, which the investors overweight. This demand makes positively skewed securities overpriced and likely to earn low returns. In this article we test whether the size/market capitalization attribute, and associated factor-mimicking portfolios, receive a lottery-like payoff�. The implications of this are that most small stocks do not payoff� and the returns to a size strategy are driven by a small number of winners. This type of payo�ff can be captured through diversi�fication but leaves an under-diversifi�ed investor exposed. The risk being that they will not include winning stocks and their resulting return expectation is negative.
To investigate the e�ffect of winning stocks on the performance of investment portfolios based on the size we propose a conditional logit model for ranking di�fferent investment portfolios based on size and assess the robustness of the ranking to the inclusion/exclusion of the best performing stocks in the cross-section. This parametric choice is embedded within a stochastic utility model for explaining the investment decisions of under-diversi�fied size investors aiming to exploit the so-called size premium. under-diversifi�ed individuals maximize their expected utility in each period by choosing the stock that is predicted to yield the highest return (highest positive skew). This choice is driven by market capitalization of the portfolio and modeled parametrically using the conditional logit model.
In order to obtain cross-sectional variation on the relationship between the size e�ffect and portfolio performance we split the whole cross-section of stocks into di�fferent industries and fi�t the conditional logit model to each industry separately. We apply the conditional logit model at an industry-speci�fic level across three ranked sorted portfolios based on market capitalization: a small, mid-size and big portfolio created from the stocks in each tercile of the cross-section of assets in a speci�fic industry ranked by asset size. This exercise is repeated for 20 industries over the period January 1970 to November 2015. Our results reveal that the size e�ffect vanishes once the top performing stocks in an industry are removed from the sample.
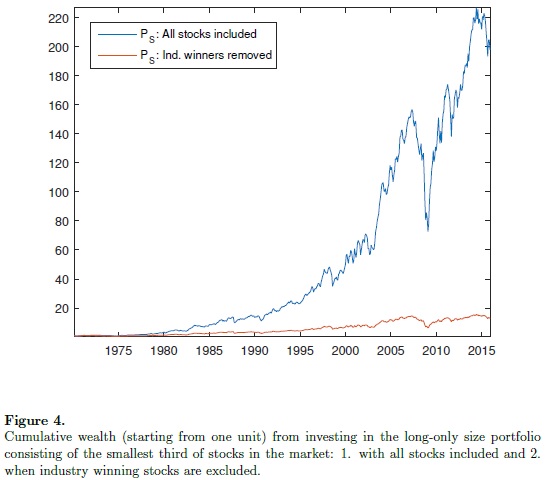
Our empirical �findings also highlight the role of industry momentum in determining the relationship between market capitalization and portfolio performance. Speci�fically, market capitalization has signi�ficantly better predictive ability for portfolio return performance in the months following a positive return in an industry than in the months following a negative industry return.
Given these �findings, we investigate further the influence of the winning stocks in industry-speci�fic size portfolios. In particular, we propose an alternative size portfolio that we denominate as the winner-weighted index, based on the forecast rank probabilities of stocks provided by the conditional logit model. Intuitively, those stocks that are predicted to be winners in the next period receive a larger allocation of wealth than those stocks that have a low probability of becoming winners. More formally, the allocation of wealth to each asset in the portfolio is determined by the forecast winning probabilities obtained from the conditional logit model and driven by asset size. The performance of this portfolio is compared against a cap-weighted index benchmark portfolio. The weights in the latter portfolio are also driven by market capitalization, however, in contrast to our winner-weighted index portfolio, smaller stocks within an industry receive a smaller allocation of wealth. We consider statistical and economic measures such as the Sharpe ratio, Sortino ratio, the certainty equivalent return of a mean-variance investor and portfolio turnover. We observe the existence of two regimes in portfolio performance. During positive industry momentum periods, the winner-weighted index outperforms the cap-weighted portfolio for 19 out of 20 industries, the exception being the utilities industry. This result is, however, reversed in periods of negative industry momentum for which the cap-weighted index outperforms the winner-weighted index in 18 out of 20 industries.
Our second objective is to explore the influence of winning stocks on the size portfolio pricing factor widely used in the empirical asset pricing literature. Our empirical results for both a top-minus-bottom trading portfolio and a long-only portfolio show that standard asset pricing models are not able to adequately capture the contribution of the size premium to the overall risk premium when the winning stocks are removed from the size factor portfolio. In contrast, we note that the factor loadings (�Beta’s) associated to the size portfolio pricing factor in standard models are robust to the inclusion/exclusion of the winning stocks. The removal of winning stocks is a�ffecting the risk premium rather than the covariance of portfolios with the risk factor.”
Are you looking for more strategies to read about? Check http://quantpedia.com/Screener
Do you want to see an overview of our database of trading strategies? Check https://quantpedia.com/Chart
Do you want to know how we are searching new strategies? Check https://quantpedia.com/Home/How
Do you want to know more about us? Check http://quantpedia.com/Home/About
Follow us on:
Facebook: https://www.facebook.com/quantpedia/
Twitter: https://twitter.com/quantpedia
Share onLinkedInTwitterFacebookRefer to a friend

























