The net current asset value (NCAV/MV) strategy is the famous strategy popularized (and used) by the father of security analysis, Benjamin Graham, in the early twentieth century, bringing high profits from the 1930s to 1956. Per-share NCAV, as defined by Graham (Graham and Dodd (1934), Graham (1976)), is the balance sheet current assets minus all the firm’s (current and long-term) liabilities divided by the number of shares outstanding. Long-term assets (e.g., intangible assets and fixed assets) values are not counted.
Graham found that companies satisfying the NCAV/MV strategy were often priced at significant discounts to estimates the value that stockholders could receive in the event of the actual sale or liquidation of the entire corporation. Thus, the NCAV/MV rule not only protects capital from significant permanent loss but also generates a portfolio of stocks with excellent prospects for an advance in price.
* For those interested in systematic quantitative value factor ETF implementation, here is a link to the Alpha Architect Quantitative Value ETF (strategy background), our partner. *
The NCAV rule forms portfolios filled with stocks with market capitalization lower than the amount of cash plus inventories they own.
A lot of these stocks are so cheap because the companies are in distress and will eventually go bankrupt. But the rest of the stocks bought with an extreme discount statistically gain more, and the overall portfolio return is highly positive.
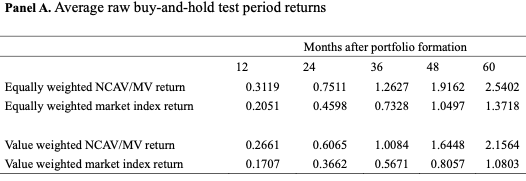
per annum, long only portfolio, benchmark market return 20,51% (data from table 2 panel A, equally weighted stocks)
not stated
more or less, it depends on investor’s need for diversification
not stated
The investment universe consists of all stocks on the London Exchange. Companies with more than one class of ordinary shares and foreign companies are excluded. Also excluded are companies on the lightly regulated markets and companies which belong to the financial sector. The portfolio of stocks is formed annually in July. Only those stocks with an NCAV/MV higher than 1.5 are included in the NCAV/MV portfolio. This Buy-and-hold portfolio is held for one year. Stocks are weighted equally.
No - Long-only value stocks logically can’t be used as a hedge against market drops as a lot of strategy’s performance comes from equity market premium (as the investor holds equities, therefore, his correlation to the broad equity market is very very high). Now, evidence for using a long-short value factor portfolio as a hedge against the equity market is very mixed. Firstly, there are a lot of definitions of value factor (from simple standard P/B ratios to various more complex definitions as in this strategy), and the performance of different value factors differ in times of stress. Also, there are multiple research papers in a tone of work of Cakici and Tan : “Size, Value, and Momentum in Developed Country Equity Returns: Macroeconomic and Liquidity Exposures” that link value factor premium to liquidity and growth risk and show that the implication is that value returns can be low prior to periods of low global economic growth and bad liquidity.
