Related to all major factor strategies (trend, momentum, value, carry, seasonality and low beta/volatility):

Authors: Baltussen, Swinkels, van Vliet

Title: Global Factor Premiums

Link: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3325720

Abstract:

We examine 24 global factor premiums across the main asset classes via replication and new-sample evidence spanning more than 200 years of data. Replication yields ambiguous evidence within a unified testing framework with methods that account for p-hacking. The new-sample evidence reveals that the large majority of global factors are strongly present under conservative p-hacking perspectives, with limited out-of-sample decay of the premiums. Further, utilizing our deep sample, we find global factor premiums to be not driven by market, downside, or macroeconomic risks. These results reveal strong global factor premiums that present a challenge to asset pricing theories.

Notable quotations from the academic research paper:

"In this paper we study global factors premiums over a long and wide sample spanning the recent 217 years across equity index (but not single securities), bond, currency, and commodity markets.

The first objective of this study is to robustly and rigorously examine these global factor premiums from the perspective of ‘p-hacking’.

We take as our starting point the main global return factors published in the Journal of Finance and the Journal of Financial Economics during the period 2012-2018: time-series momentum (henceforth ‘trend’), cross-sectional momentum (henceforth ‘momentum’), value, carry, return seasonality and betting-against-beta (henceforth ‘BAB’). We examine these global factors in four major asset classes: equity indices, government bonds, commodities and currencies, hence resulting in a total of 24 global return factors.4

We work from the idea that these published factor premiums could be influenced by p-hacking and that an extended sample period is useful for falsification or verification tests. Figure 1, Panel A summarizes the main results of these studies.

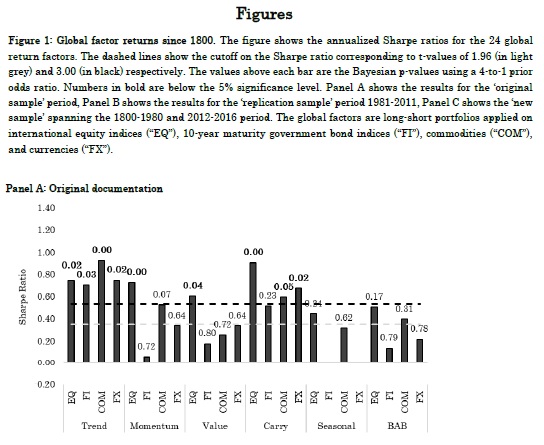
Shown are the reported Sharpe ratio’s in previous publications, as well as the 5% significance cutoff in the grey-colored dashed line. In general, the studies show evidence on the global factor premiums, with 14 of the 22 factors (return seasonality is not tested in bonds and currencies) displaying significant Sharpe ratio’s at the conventional 5% significance level.

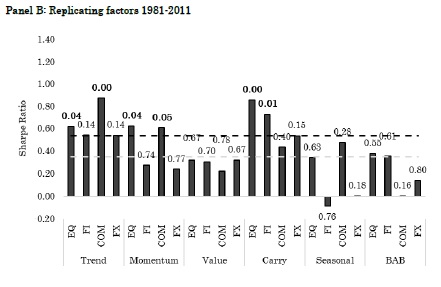
Further, most of the studies have differences in, amongst others, testing methodologies, investment universes and sample periods, choices that introduce degrees of freedom to the researcher. To mitigate the impact of such degrees of freedom, we reexamine the global return factors using uniform choices on testing methodology and investment universe over their average sample period (1981-2011). Figure 1, Panel B shows the results of this replicating exercise. We find that Sharpe ratios are marginally lower, with 12 of the 24 factor premiums being significant at the conventional 5% level.

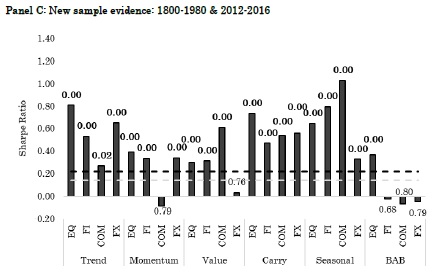
The second objective of this study is to provide rigorous new sample evidence on the global return factors. To this end, we construct a deep, largely uncovered historical global database on the global return factors in the four major asset classes. This data consists of pre-sample data spanning the period 1800- 1980, supplemented with post-sample data from 2012-2016, such that we have an extensive new sample to conduct further analyses. If the global return factors were unintentionally the result of p-hacking, we would expect them to disappear for this new sample period.

Our new sample findings reveal consistent and ubiquitous evidence for the large majority of global return factors. Figure 1, Panel C summarizes our main findings by depicting the historical Sharpe ratio’s in the new sample period. In terms of economic significance, the Sharpe ratios are substantial, with an average of 0.41. Remarkably, in contrast to most out-of-sample studies we see very limited ‘out-of-sample’ decay of factor premiums.

In terms of statistical significance and p-hacking perspectives, 19 of the 24 t-values are above 3.0,19 Bayesian p-values are below 5%, and the break-even prior odds generally need to be above 9,999 to have less than 5% probability that the null hypothesis is true."

Are you looking for more strategies to read about? Check http://quantpedia.com/Screener

Do you want to see performance of trading systems we described? Check http://quantpedia.com/Chart/Performance

Do you want to know more about us? Check http://quantpedia.com/Home/About

Follow us on:

Facebook: https://www.facebook.com/quantpedia/

Twitter: https://twitter.com/quantpedia

Benjamin Franklin once said "… in this world nothing can be said to be certain, except death and taxes." and we completely agree with that quote. Traders and portfolio managers often strongly concentrate on a process of building the strategy which delivers the highest outperformance. But a lot of them forget to include taxes into that building process. And this can be a significant mistake as the following research paper shows:

Authors: Goldberg, Hand, Cai

Title: Tax-Managed Factor Strategies

Link: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3309974

Abstract:

We examine the tax efficiency of an indexing strategy and six factor tilts. Between June 1995 and March 2018, average value added by tax management exceeded 1.4% per year at a 10- year horizon for all the strategies we considered. Tax-managed factor tilts that are beta 1 to the market generated average tax alpha between 1.6% and 1.9% per year, while average tax alpha for the tax-managed indexing strategy was 2.3% per year. These remarkable results depend on the availability of short-term capital gains to offset. To a great extent, they can be attributed to loss harvesting and the tax rate differential.

Notable quotations from the academic research paper:

"In 1993, Rob Jeffrey and Rob Arnott asked a provocative question: Is an investor’s alpha big enough to cover its taxes? Arnott and Jeffrey pointed out that alpha generation typically requires high turnover, which erodes pre-tax alpha by increasing taxes, but this important fact tended to be overlooked by investors and researchers. Twenty-five years later, the situation has not changed too much.

Some principles of tax-aware investing, such as locating high-tax investments in tax-deferred accounts or using tax-free municipal bonds (instead of their taxable counterparts) as investments and benchmarks, are no more than common sense. Other principles of taxaware investing may rely on more sophisticated mathematics and economics, as well as more detailed knowledge of the complex and ever-changing US tax code. An example of the latter would be loss harvesting, which is a tax-aware option that combines delayed realization of capital gains with immediate realization of capital losses. A second timing option, which depends on the tax rate differential, involves the realization of long-term gains in order to facilitate the harvesting of short-term losses.

In the present study, we document the performance of after-tax return and risk profiles of an indexing strategy and six factor tilts over the period June 1995 to March 2018.7 We focus on active return, and our results rely on a number of methodological innovations. We mitigate the substantial impact of period dependence on results by launching each strategy at regular intervals over a long horizon, generating ranges of outcomes obtained in different market climates. We construct each portfolio with a one-step optimization that balances the competing imperatives of constraining factor exposures, harvesting losses, and minimizing tracking error (TE) to a diversified benchmark. We develop an after-tax performance attribution scheme that decomposes estate/donation and liquidation active returns into factor alpha, tax alpha, and tracking return. We measure the impact of the tax rate differential that affects tax-managed factor tilts.

Our results span several dimensions. First, we compare after-tax performance of tax-managed versions to tax-indifferent versions of each strategy. In back-tests, average value added by tax management during the period studied exceeded 1.50% per year at 10-year horizon for all the strategies we considered. This finding illustrates the potential power of loss harvesting and lets us move on to the more nuanced topic of the loss-harvesting capacities of different strategies.

Figure 1 presents the average after-tax active return of the tax-managed versions of the strategies graphically. Overall, the best average performance was delivered by the Small Value strategy, but more than half the after-tax active return was due to factor alpha. On the basis of tax alpha, the strategies divide into the three groups. The highest average tax alpha was delivered by the indexing strategy. Each of the four beta-1 strategies captured at least 70% of the tax alpha in the indexing strategy, but the two lower-risk strategies captured less than 35%. The division is marked in the performance charts."

Are you looking for more strategies to read about? Check http://quantpedia.com/Screener

Do you want to see an overview of our database of trading strategies? Check https://quantpedia.com/Chart

Do you want to know how we are searching new strategies? Check https://quantpedia.com/Home/How

Do you want to know more about us? Check http://quantpedia.com/Home/About

Follow us on:

Facebook: https://www.facebook.com/quantpedia/

Twitter: https://twitter.com/quantpedia

A new research paper related mainly to:

#26 – Value (Book-to-Market) Anomaly

Authors: Zhou

Title: Can Cash-Flow Beta Explain the Value Premium?

Link: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3244791

Abstract:

It is well documented that the cash flow beta can partly explain the source of the value premium. This paper presents an empirical test that cast doubt on this widely accepted belief. We double sort the stocks with their value and quality dimension and obtain four corner portfolios: (A) expensive quality, (B) cheap junk, (C) cheap quality and (D) expensive junk stocks. Prior research has shown that the value premium concentrates on cheap quality minus expensive junk (i.e. undervalued minus overvalued) but is not significant in cheap junk minus expensive quality stocks. If cash-flow beta is the source of the value premium, we would expect a larger cash-flow beta difference between the cheap quality and expensive junk portfolio. However, our empirical test shows that β_CF ((B) cheap junk) – β_CF ((A) expensive quality) >>β_CF ((C) cheap quality)-β_CF ((D) expensive junk). In other words, B minus A does not contribute to the profit of the value premium but contribute most to the difference of the cash flow beta between value and growth portfolios. Therefore, our result may serve as evidence that the cash flow beta may only spuriously explain the value premium. Or, at least, the cash-flow risk premium estimated in the portfolio regression approach is biased.

Notable quotations from the academic research paper:

"The value premium is one of the most important anomalies in the field of asset pricing. It is well known that the market beta fails to explain the value premium in the dataset after 1963.

Campbell and Vuolteenaho (2004) first proposed a “good beta, bad beta” model to solve this dilemma. They decompose the traditional market beta into two components: A good beta is the beta that measures a stock’s covariance with the temporary market movement or discount rate news, which is usually induced by changing market sentiment and varying risk aversion; A bad beta measures a stock’s comovement with market-wide fundamental cash-flow news. Campbell and Vuolteenaho (2004) and Cohen, Polk, Vuolteenaho(2009) argue that investors will regard wealth decrease induced by discount rate news as less significant because it tends to be temporary and the investors will be compensated by better future investment opportunity in an increased discount rate environment. A rational investor will demand higher return for the bad beta than the good beta.

Together with Campbell and Vuolteenaho (2004), Cohen, Polk, Vuolteenaho(2009), Campbell, Polk and Vuolteenaho (2010) and Da and Warachka (2009) among others, use different proxy for the cash-flow news and find that value stocks have a higher cash-flow beta than growth stocks. They conclude that cash-flow beta is one of the sources of the value premium. In this paper, we present an empirical test that question this widely accepted belief.

Our test double-sorts the stocks by value and quality dimension. In a conceptual simplified picture, Figure 1 illustrates four groups of stocks: (A) high quality, high price (expensive quality), (B) low quality, low price (cheap junk), (C) high quality, low price (cheap quality), and (D) low quality, high price (expensive junk). The price of portfolio A and B is thought to be “right” as their price is more aligned with the quality. Portfolio C (D) is the undervalued (overvalued) stocks.

High price portfolio A and D are growth stocks, and low price portfolio B and C are value stocks. The value premium is the return of ( + ) − ( + ) = ( − ) + ( − ) . ( − ) and ( − ) are represented respectively by the light blue and dark blue arrow in Figure 1.

When the price is “right”, the value premium is not significant. The value premium is concentrated on ( − ), but not on ( − ). The return of the four portfolio have the relationship: R > R ≈ R > R .

If the cash flow beta is the source of the value premium and the value premium is concentrated on ( − ), one would naturally expect that f( ) − f( ) ≫ f( ) − f( ), in which, f is the cash flow beta. However, in our
test, we find the opposite results: f( ) − f( ) ≫ f( ) − f( ). ( − ) does not contribute to the profit of the value premium while f( ) − f( ) contribute the most to the cash-flow beta difference between the value and growth portfolio.

If the cash-flow beta represents a risk, we take most of the risk in the value-junk minus growth quality portfolio, but we earn no profit or even negative profit. We take very little or negative risk in the value-quality minus growth-junk portfolio, but we earn most of the profit of the value premium. We need to find a plausible explanation to this phenomena before we conclude that the cash-flow risk is the source of the value premium. A fundamental reason of our result is that, on the value dimension, higher return links to a higher cash-flow beta, while on the quality dimension, higher return links to a lower cash-flow beta."

Are you looking for more strategies to read about? Check http://quantpedia.com/Screener

Do you want to see an overview of our database of trading strategies? Check https://quantpedia.com/Chart

Do you want to know how we are searching new strategies? Check https://quantpedia.com/Home/How

Do you want to know more about us? Check http://quantpedia.com/Home/About

Follow us on:

Facebook: https://www.facebook.com/quantpedia/

Twitter: https://twitter.com/quantpedia

A new research paper related mainly to:

#77 – Beta Factor in Stocks

Authors: Novy-Marx, Velikov

Title: Betting Against Betting Against Beta

Link: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3300965

Abstract:

Frazzini and Pedersen’s (2014) Betting Against Beta (BAB) factor is based on the same basic idea as Black’s (1972) beta-arbitrage, but its astonishing performance has generated academic interest and made it highly influential with practitioners. This performance is driven by non-standard procedures used in its construction that effectively, but non-transparently, equal weight stock returns. For each dollar invested in BAB, the strategy commits on average $1.05 to stocks in the bottom 1% of total market capitalization. BAB earns positive returns after accounting for transaction costs, but earns these by tilting toward profitability and investment, exposures for which it is fairly compensated. Predictable biases resulting from the paper’s non-standard beta estimation procedure drive results presented as evidence supporting its underlying theory.

Notable quotations from the academic research paper:

" Frazzini and Pedersen’s (FP) Betting Against Beta (BAB, 2014) is an unmitigated academic success. Despite being widely read, and based on a fairly simple idea, BAB is not well understood. This is because the authors use three unconventional procedures to construct their factor. All three departures from standard factor construction contribute to the paper’s strong empirical results. None is important for understanding the underlying economics, and each obscures the mechanisms driving reported effects.

Two of these non-standard procedures drive BAB’s astonishing “paper” performance, which cannot be achieved in practice, while the other drives results FP present as evidence supporting their theory. The two responsible for driving performance can be summarized as follows:

Non-standard procedure #1, rank-weighted portfolio construction: Instead of simply sorting stocks when constructing the beta portfolios underlying BAB, FP use a “rank-weighting” procedure that assigns each stock to either the “high” portfolio or the “low” portfolio with a weight proportional to the cross-sectional deviation of the stock’s estimated beta rank from the median rank.

Non-standard procedure #2, hedging by leveraging: Instead of hedging the low beta-minus-high beta strategy underlying BAB by buying the market in proportion to the underlying strategy’s observed short market tilt, FP attempt to achieve market-neutrality by leveraging the low beta portfolio and deleveraging the high beta portfolio using these portfolios’ predicted betas, with the intention that the scaled portfolios’ betas are each equal to one and thus net to zero in the long/short strategy.

FP’s first of these non-standard procedures, rank-weighting, drives BAB’s performance not by what it does, i.e., put more weight on stocks with extreme betas, but by what it does not do, i.e., weight stocks in proportion to their market capitalizations, as is standard in asset pricing. The procedure creates portfolios that are almost indistinguishable from simple, equal-weighted portfolios. Their second non-standard procedure, hedging with leverage, uses these same portfolios to hedge the low beta-minus-high beta strategy underlying BAB. That is, the rank-weighting procedure is a backdoor to equal-weighting the underlying beta portfolios, and the leveraging procedure is a backdoor to using equal-weighted portfolios for hedging.

BAB achieves its high Sharpe ratio, and large, highly significant alpha relative to the common factor models, by hugely overweighting micro- and nano-cap stocks. For each dollar invested in BAB, the strategy commits on average $1.05 to stocks in the bottom 1% of total market capitalization. These stocks have limited capacity and are expensive to trade. As a result, while BAB’s “paper” performance is impressive, it is not something an investor can actually realize. Accounting for transaction costs reduces BAB’s profitability by almost 60%. While it still earns significant positive returns, it earns these by tilting toward profitability and investment, exposures for which it is fairly compensated."

Are you looking for more strategies to read about? Check http://quantpedia.com/Screener

Do you want to see an overview of our database of trading strategies? Check https://quantpedia.com/Chart

Do you want to know how we are searching new strategies? Check https://quantpedia.com/Home/How

Do you want to know more about us? Check http://quantpedia.com/Home/About

Follow us on:

Facebook: https://www.facebook.com/quantpedia/

Twitter: https://twitter.com/quantpedia

A new research paper related mainly to:

#25 – SIze Premium

Authors: McGee, Olmo

Title: The Size Premium As a Lottery

Link: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3279645

Abstract:

We investigate empirically the dependence of the size effect on the top performing stocks in a cross-section of risky assets separated by industry. We propose a test for a lottery-style factor payoff based on a stochastic utility model for an under-diversified investor. The associated conditional logit model is used to rank different investment portfolios based on size and we assess the robustness of the ranking to the inclusion/exclusion of the best performing stocks in the cross-section. Our results show that the size effect has a lottery-style payoff and is spurious for most industries once we remove the single best returning stock in an industry from the sample each month. Analysis in an asset pricing framework shows that standard asset pricing models fail to correctly specify the size premium on risky assets when industry winners are excluded from the construction of the size factor. Our findings have implications for stock picking, investment management and risk factor analysis.

Notable quotations from the academic research paper:

" Firms with small market capitalization tend to outperform larger companies. Investors are attracted to lottery-like assets with positively skewed returns because they offer a very large payoff with a small probability, which the investors overweight. This demand makes positively skewed securities overpriced and likely to earn low returns. In this article we test whether the size/market capitalization attribute, and associated factor-mimicking portfolios, receive a lottery-like payoff. The implications of this are that most small stocks do not payoff and the returns to a size strategy are driven by a small number of winners. This type of payoff can be captured through diversification but leaves an under-diversified investor exposed. The risk being that they will not include winning stocks and their resulting return expectation is negative.

To investigate the effect of winning stocks on the performance of investment portfolios based on the size we propose a conditional logit model for ranking different investment portfolios based on size and assess the robustness of the ranking to the inclusion/exclusion of the best performing stocks in the cross-section. This parametric choice is embedded within a stochastic utility model for explaining the investment decisions of under-diversified size investors aiming to exploit the so-called size premium. under-diversified individuals maximize their expected utility in each period by choosing the stock that is predicted to yield the highest return (highest positive skew). This choice is driven by market capitalization of the portfolio and modeled parametrically using the conditional logit model.

In order to obtain cross-sectional variation on the relationship between the size effect and portfolio performance we split the whole cross-section of stocks into different industries and fit the conditional logit model to each industry separately. We apply the conditional logit model at an industry-specific level across three ranked sorted portfolios based on market capitalization: a small, mid-size and big portfolio created from the stocks in each tercile of the cross-section of assets in a specific industry ranked by asset size. This exercise is repeated for 20 industries over the period January 1970 to November 2015. Our results reveal that the size effect vanishes once the top performing stocks in an industry are removed from the sample.

Our empirical findings also highlight the role of industry momentum in determining the relationship between market capitalization and portfolio performance. Specifically, market capitalization has significantly better predictive ability for portfolio return performance in the months following a positive return in an industry than in the months following a negative industry return.

Given these findings, we investigate further the influence of the winning stocks in industry-specific size portfolios. In particular, we propose an alternative size portfolio that we denominate as the winner-weighted index, based on the forecast rank probabilities of stocks provided by the conditional logit model. Intuitively, those stocks that are predicted to be winners in the next period receive a larger allocation of wealth than those stocks that have a low probability of becoming winners. More formally, the allocation of wealth to each asset in the portfolio is determined by the forecast winning probabilities obtained from the conditional logit model and driven by asset size. The performance of this portfolio is compared against a cap-weighted index benchmark portfolio. The weights in the latter portfolio are also driven by market capitalization, however, in contrast to our winner-weighted index portfolio, smaller stocks within an industry receive a smaller allocation of wealth. We consider statistical and economic measures such as the Sharpe ratio, Sortino ratio, the certainty equivalent return of a mean-variance investor and portfolio turnover. We observe the existence of two regimes in portfolio performance. During positive industry momentum periods, the winner-weighted index outperforms the cap-weighted portfolio for 19 out of 20 industries, the exception being the utilities industry. This result is, however, reversed in periods of negative industry momentum for which the cap-weighted index outperforms the winner-weighted index in 18 out of 20 industries.

Our second objective is to explore the influence of winning stocks on the size portfolio pricing factor widely used in the empirical asset pricing literature. Our empirical results for both a top-minus-bottom trading portfolio and a long-only portfolio show that standard asset pricing models are not able to adequately capture the contribution of the size premium to the overall risk premium when the winning stocks are removed from the size factor portfolio. In contrast, we note that the factor loadings (Beta's) associated to the size portfolio pricing factor in standard models are robust to the inclusion/exclusion of the winning stocks. The removal of winning stocks is affecting the risk premium rather than the covariance of portfolios with the risk factor."

Are you looking for more strategies to read about? Check http://quantpedia.com/Screener

Do you want to see an overview of our database of trading strategies? Check https://quantpedia.com/Chart

Do you want to know how we are searching new strategies? Check https://quantpedia.com/Home/How

Do you want to know more about us? Check http://quantpedia.com/Home/About

Follow us on:

Facebook: https://www.facebook.com/quantpedia/

Twitter: https://twitter.com/quantpedia