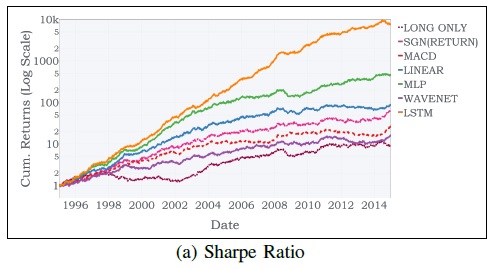
The Best of Strategies for the Times of Crisis
We at Quantpedia are not the only ones who are interested in finding strategies that can be used to mitigate the impacts of the large equity corrections. We have already written a short article about a lottery/skewness strategy in commodities, which offers some protection in a time of crisis. Our users can also screen a list of strategies that can be used as a hedge/diversification for equity markets during downturns. A new research paper written by Harvey, Hoyle, Rattray, Sargaison, Taylor and Van Hemert explores the same question and analyzes the performance of different tools that investors could deploy during equity bear markets. We sincerely recommend it …
Authors: Harvey, Hoyle, Rattray, Sargaison, Taylor, Van Hemert
Title: The Best of Strategies for the Worst of Times: Can Portfolios be Crisis Proofed?
Link: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3383173
Abstract:
In the late stages of long bull markets, a popular question arises: What steps can an investor take to mitigate the impact of the inevitable large equity correction? However, hedging equity portfolios is notoriously difficult and expensive. We analyze the performance of different tools that investors could deploy. For example, continuously holding short-dated S&P 500 put options is the most reliable defensive method but also the most costly strategy. Holding ‘safe-haven’ US Treasury bonds produces a positive carry, but may be an unreliable crisis-hedge strategy, as the post-2000 negative bond-equity correlation is a historical rarity. Long gold and long credit protection portfolios sit in between puts and bonds in terms of both cost and reliability. Dynamic strategies that performed well during past drawdowns include: futures time-series momentum (which benefits from extended equity sell-offs) and a quality strategy that takes long/short positions in the highest/lowest quality company stocks (which benefits from a ‘flight-to-quality’ effect during crises). We examine both large equity drawdowns and recessions. We also provide some out-of-sample evidence of the defensive performance of these strategies relative to an earlier, related paper.
Notable quotations from the academic research paper:
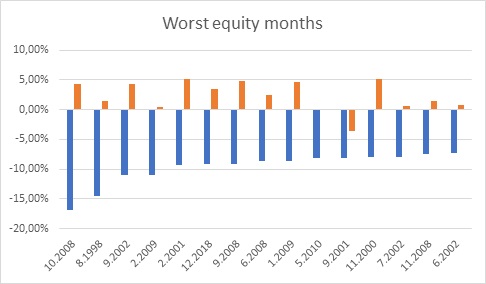
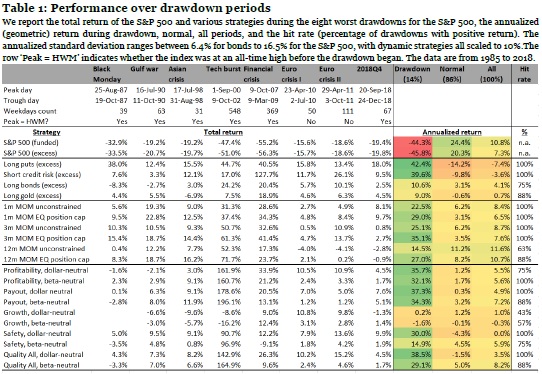
"The typical investment portfolio is highly concentrated in equities leaving investors vulnerable to large drawdowns. We examine the performance of a number of candidate defensive strategies, both active and passive, between 1985 and 2018, with a particular emphasis on the eight worst drawdowns (the instances where the S&P 500 fell by more than 15%) and three US recessions. To guard against overfitting, we provide out-of-sample evidence of the performance of these strategies in the 2018Q4 drawdown that occurred after we wrote an earlier, related paper.
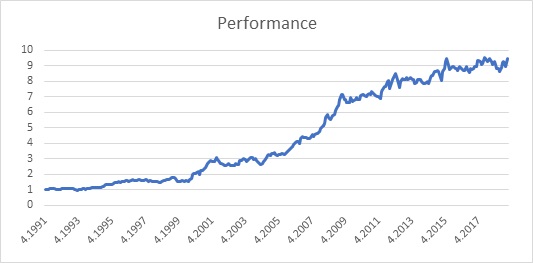
We begin with two passive strategies, both of which benefit directly from a falling equity market. A strategy that buys, and then rolls, one-month S&P 500 put options performs well in each of the eight equity drawdown periods. However, it is very costly during the ‘normal’ times, which constitute 86% of our sample and expansionary (non-recession) times, which constitute 93% of our observations. As such, passive option protection seems too expensive to be a viable crisis hedge. A strategy that is long credit protection (short credit risk) also benefits during each of the eight equity drawdown periods, but in a more uneven manner, doing particularly well during the 2007-2009 Financial Crisis, which was a credit crisis. Nevertheless, the credit protection strategy is less costly during normal times and non-recessions than the put buying strategy.
Next, we consider so-called ‘safe-haven’ investments. A strategy that holds long positions in 10-year US Treasuries performed well in the post-2000 equity drawdowns, but was less effective during previous equity sell-offs. This is consistent with the negative bond-equity correlation witnessed post-2000, which is atypical from the longer historical perspective. As we move beyond the extreme monetary easing that has characterized the post-Financial Crisis period, it is possible that the bond-equity correlation may revert to the previous norm, rendering a long bond strategy a potentially unreliable crisis hedge. A long gold strategy generally performs better during crisis periods than at normal times, consistent with its reputation as a safe-haven security. However, its appeal as a crisis hedge is diminished by the fact that its long-run return, measured over the 1985-2018 period, is close to zero and that it carries substantial idiosyncratic risk unrelated to equity markets.
We then turn our attention to dynamic strategies.
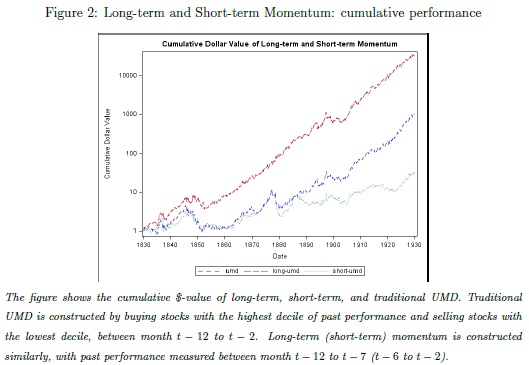
Time-series momentum strategies add to winning positions (ride winners) and reduce losing positions (cut losers), much like a dynamic replication of an option straddle strategy. We show that such strategies performed well over the eight equity drawdowns and three recessions. We also explore limiting the equity exposure (no long positions allowed), which we find enhances the crisis performance.
Next, we consider long-short US equity strategies. A review of the factors proposed in the academic literature suggests that those that take long positions in high-quality and short positions in low-quality companies are most promising as crisis hedges, since they benefit from flights to quality when panic hits markets. The definition of a quality business is, of course, open to debate. However, broadly speaking, such companies will be profitable, growing, have safer balance sheets, and run investor-friendly policies in areas such as payout ratios. We examine a host of quality metrics, and illustrate the importance of a beta-neutral (common in practice) rather than a dollar-neutral (common in academic studies) portfolio construction.

"
Are you looking for more strategies to read about? Check http://quantpedia.com/Screener
Do you want to see performance of trading systems we described? Check http://quantpedia.com/Chart/Performance
Do you want to know more about us? Check http://quantpedia.com/Home/About
Follow us on:
Facebook: https://www.facebook.com/quantpedia/
Twitter: https://twitter.com/quantpedia
Youtube: https://www.youtube.com/channel/UC_YubnldxzNjLkIkEoL-FXg