Three Methods to Fix Momentum Crashes
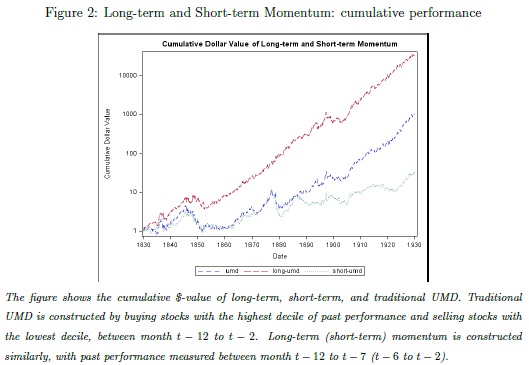
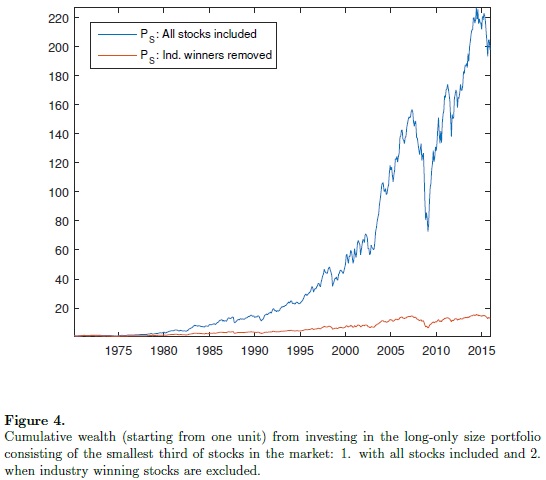
Everyone who lived during the 2007 and 2009 crisis knows what the biggest weakness of the equity momentum strategy was. It was right during the spring of 2009 when the financial markets were on its inflection point when the momentum strategy crashed. Right after that inflection point, stocks which were the biggest losers during the previous year performed exceptionally well and caused strong under-performance of classical long-short momentum strategy. How can we prevent this situation from happening again? That’s the topic of our favorite new recent study written by Matthias Hanauer and Steffen Windmueller. They analyze three momentum risk management techniques – idiosyncratic momentum, constant volatility-scaling, and dynamic scaling, to find the remedy for momentum crashes. It’s our recommended read for this week for equity long-short managers …
Authors: Matthias Hanauer and Steffen Windmueller
Title: Enhanced Momentum Strategies