Are Currently Used Significance Levels for Investment Strategies Too Strict?
Authors: de Prado, Lewis
Title: What is the Optimal Significance Level for Investment Strategies?
Link: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3193697
Abstract:
Most papers in the financial literature estimate the p-value associated with an investment strategy, without reporting the power of the test used to make that discovery. This is a mistake, because a particularly low false positive rate (Type I error) may be achieved at the expense of missing a large proportion of the investment opportunities (Type II error). In this paper we provide analytic estimates to Type I and Type II errors in the context of investments, and derive the familywise significance level that optimizes the performance of hypothesis tests under general assumptions. Contrary to long-held beliefs, we conclude that a familywise significance level below 15% is suboptimal (excessively conservative) in the context of most investment strategies.
Notable quotations from the academic research paper:
"Financial researchers conduct thousands (if not millions) of backtests before identifying an investment strategy. Hedge funds interview hundreds of portfolio managers before filling a position. Asset allocators interview thousands of asset managers before building a template portfolio with those candidates that exceed some statistical criteria. What all these examples have in common is that statistical tests are applied multiple times. When the rejection threshold is not adjusted for the number of trials (the number of times the test has been administered), false positives (Type I errors) occur with a probability higher than expected.
Empirical studies in economics and finance often fail to report the power of the test used to make a particular discovery. Without that information, readers cannot assess the rate at which false negatives occur (Type II errors). Suppose that you are a senior researcher at the Federal Reserve Board of Governors, and you are tasked with testing the hypothesis that stock prices are in a bubble. At first, you apply a high significance level, because before making a claim that might trigger draconian monetary policy actions you want to be extremely confident. At a 99% confidence level, you cannot reject the null hypothesis that stock prices are not in a bubble. When you report your findings to the Board, the chairperson asks what is the power of the test. Surprised by the unexpected request, you promise that you will report the test’s true positive probability in the next meeting. Back at your office, you are shocked to realize that, unbeknownst to you, the test’s power is only 50%. In other words, the test is so conservative that it misses half of the bubbles. At the next meeting, the chairperson shakes his head while explaining that, from the Fed’s perspective, missing half of the bubbles is much worse than taking a 1% risk of triggering a false alarm.
In contrast, hedge funds are often more concerned with false positives than with false negatives. Client redemptions are more likely to be caused by the former than the latter. Also, investors know that performance fees incentivize managers to avoid false negatives, hence a “safety first” principle calls for investors to focus on avoiding false investment strategies. Although this is a valid argument, it is unclear why investors and hedge funds would apply arbitrary significance levels, such as 10% or 5% or 1%. Rather, an objective significance level could be set such that Type I and Type II errors are jointly minimized. In other words, even researchers who do not particularly care for Type II errors could compute them as a way to introduce objectivity to an otherwise subjective choice of significance level.
The purpose of this paper is threefold: First, we provide an analytic estimate to the probability of selecting a false investment strategy, corrected for multiple testing. Second, we provide an analytic estimate to the probability of missing a true investment strategy, corrected for multiple testing. Third, we derive the significance level that maximizes the performance of a statistical test used to detect investment strategies.
WHAT IS A REASONABLE SIGNIFICANCE LEVEL FOR INVESTMENT STRATEGIES?
For the particular numerical example presented earlier, where ≈2.4978 and the true Sharpe ratio was assumed to be ∗≈0.0632 (annualized Sharpe ratio of 1.0), the harmonic mean between confidence and power is maximized at ∗ ≈0.3051 and ≈0.4224, where â„Ž≈0.6309. Exhibit 2 plots â„Ž (y-axis) as a function of (x-axis).
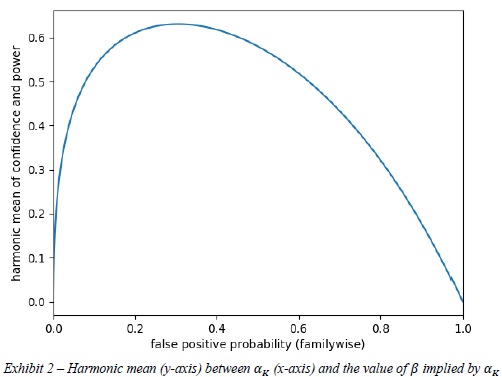
The reader may be surprised to learn that the optimal significance level is so high, compared to the standard 5% false positive rate used throughout the academic literature. The reason is, at the standard significance level of =0.05, the test is so powerless that it misses over 71.55% of strategies with a true Sharpe ratio below 1! It is therefore optimal to give up some confidence in exchange for more power, even if that means accepting a false positive rate as high as 30.51%.
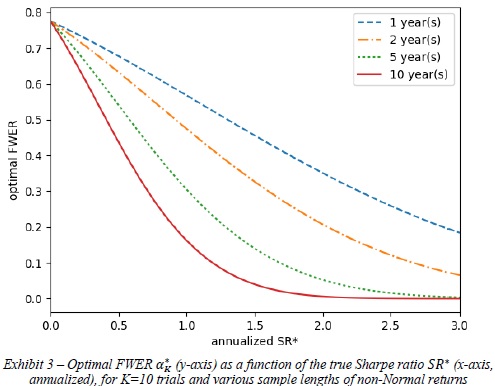
Similarly, we can compute the optimal FWER ∗ under alternative assumptions of ∗. Exhibit 3 plots the optimal ∗ (y-axis) under various ∗ values (x-axis) and sample lengths (different lines) for the same numerical example, where Ì‚=0.0791, =10, skewness is -3 and kurtosis is 10. The implication is that, unless you are researching a strategy with a true annualized Sharpe ratio above 1 over a period of more than 10 years of daily data, a FWER below 15% is likely to be excessively conservative.
"
Are you looking for more strategies to read about? Check http://quantpedia.com/Screener
Do you want to see performance of trading systems we described? Check http://quantpedia.com/Chart/Performance
Do you want to know more about us? Check http://quantpedia.com/Home/About
Follow us on:
Facebook: https://www.facebook.com/quantpedia/
Twitter: https://twitter.com/quantpedia
Share onLinkedInTwitterFacebookRefer to a friend


























