Recent advancements in machine learning have significantly enhanced the predictive accuracy of stock returns, leveraging complex algorithms to analyze vast datasets and identify patterns that traditional models often miss. The latest empirical study by Minghui Chen, Matthias X. Hanauer, and Tobias Kalsbach shows that design choices in machine learning models, such as feature selection and hyperparameter tuning, are crucial to improving portfolio performance. Non-standard errors in machine learning predictions can lead to substantial variations in portfolio returns, highlighting the importance of robust model evaluation techniques. Integrating machine learning techniques into portfolio management has shown promising results in optimizing stock returns and overall portfolio performance. Ongoing research focuses on refining these models for better financial outcomes.
Current research shows substantial differences in key design decisions, including algorithm selection, target variables, feature treatments, and training processes. This lack of consensus results in significant outcome variations and hinders comparability and replicability. To address these challenges, the authors present a systematic framework for evaluating design choices in machine learning for return prediction. They analyze 1,056 models derived from various combinations of research design choices. Their findings reveal that design choices significantly impact return predictions. The non-standard error from unsuitable choices is 1.59 times higher than the standard error.
Key findings include:
- ML returns vary substantially across design choices (see Figure 2 below).
- Non-standard errors arising from design choices exceed standard errors by 59%.
- Non-linear models tend to outperform linear models only for specific design choices.
- The authors provide practical recommendations in the form of actionable guidance for ML model design.
The study identifies the most influential design choices affecting portfolio returns. These include post-publication treatment, training window, target transformation, algorithm, and target variable. Excluding unpublished features in model training decreases monthly portfolio returns by 0.52%. An expanding training window yields a 0.20% higher monthly return than a rolling window.
Additionally, models with continuous targets and forecast combinations perform better, highlighting the importance of these design choices. The authors provide guidance on selecting appropriate decisions based on economic effects. They recommend using abnormal returns relative to the market as the target variable to achieve higher portfolio returns. Non-linear models outperform linear OLS models under specific conditions, such as continuous target returns or expanding training windows. The study emphasizes the need for careful consideration and rational justification of research design choices in machine learning.
Authors: Minghui Chen, Matthias X. Hanauer, and Tobias Kalsbach
Title: Design choices, machine learning, and the cross-section of stock returns
Link: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=5031755
Abstract:
We fit over one thousand machine learning models for predicting stock returns, systematically varying design choices across algorithm, target variable, feature selection, and training methodology. Our findings demonstrate that the non-standard error in portfolio returns arising from these design choices exceeds the standard error by 59%. Furthermore, we observe a substantial variation in model performance, with monthly mean top-minus-bottom returns ranging from 0.13% to 1.98%. These findings underscore the critical impact of design choices on machine learning predictions, and we offer recommendations for model design. Finally, we identify the conditions under which non-linear models outperform linear models.
As always, we present several bewitching figures and tables:
Notable quotations from the academic research paper:
“The main findings of our study can be summarized as follows: First, we document substantial variation in top-minus-bottom decile returns across different machine learning models. For example, monthly mean returns range from 0.13% to 1.98%, with corresponding annualized Sharpe ratios ranging from 0.08 to 1.82.
Second, we find that the variation in returns due to these design choices, i.e., the non-standard error, is approximately 1.59 times higher than the standard error from the statistical bootstrapping process.
[. . .] we contribute to studies that provide guidelines for finance research. For instance, Ince and Porter (2006) offer guidelines for handling international stock market data, Harvey et al. (2016) propose a higher hurdle for testing the significance of potential factors, and Hou et al. (2020) recommend methods for mitigating the impact of small stocks in portfolio sorts. By offering guidance on design choices for machine learning- based stock return predictions, we help reduce uncertainties in model design and enhance the interpretability of prediction results.
[. . .] study has important implications for machine learning research in finance. A deeper understanding of the critical design choices is essential for optimizing machine learning models, thereby enhancing their reliability and effectiveness in predicting stock returns. By addressing variations in research settings, our work helps researchers demon- strate the robustness of their findings and reduce non-standard errors in future studies. This, in turn, allows for more accurate and nuanced interpretations of results.
When predicting stock returns using machine learning algorithms, researchers and prac- titioners face a number of important methodological choices. We identify such variations in design choices in several published machine-learning studies, all of which predict the cross-section of stock returns. More specifically, these studies include Gu et al. (2020), Freyberger et al. (2020), Avramov et al. (2023), and Howard (2024) for U.S. market, Rasekhschaffe and Jones (2019) and Tobek and Hronec (2021) for global developed mar- kets, Hanauer and Kalsbach (2023) for emerging markets, and Leippold et al. (2022) for the Chinese market. In total, we identify variations in seven common research design choices across these studies, and we categorize them into four main types regarding the algorithm, target, feature, and training process. Table 1 summarizes the specific design choices of these studies.
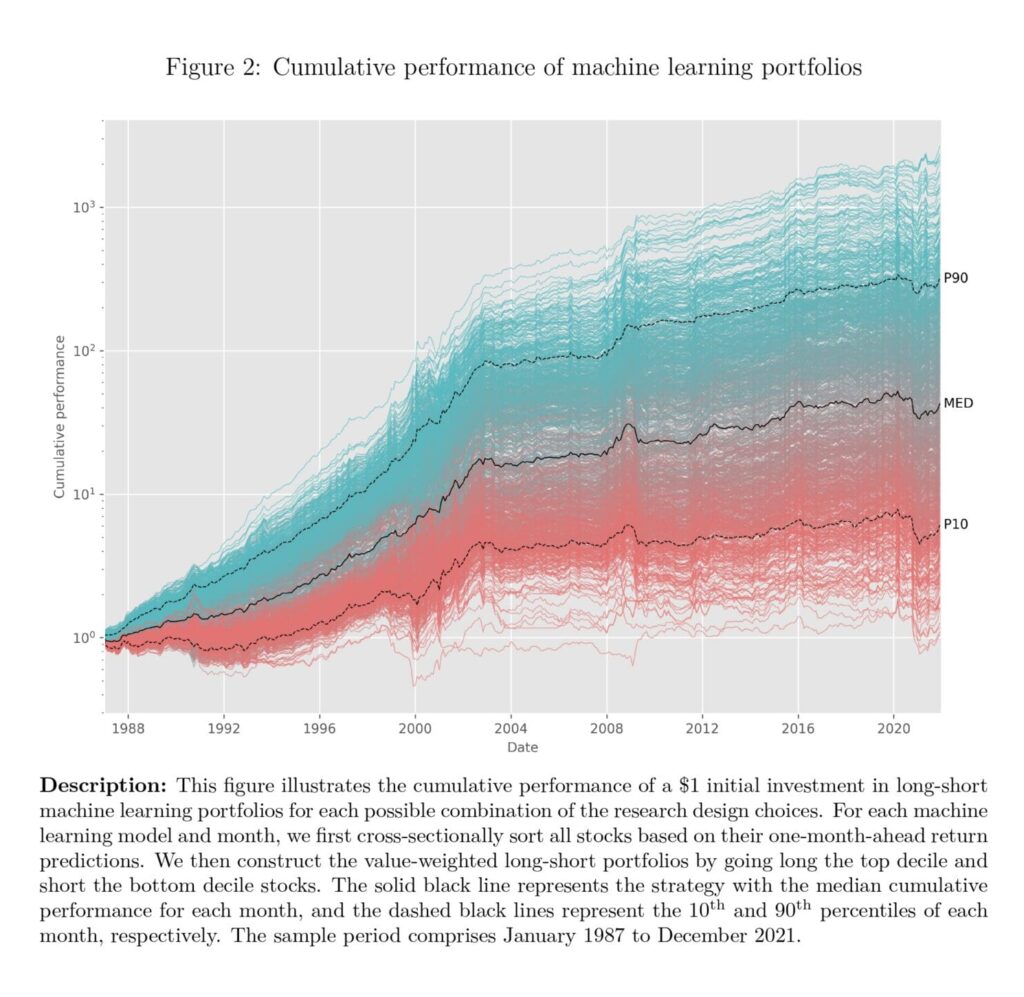
Next, we investigate the performance dispersion of the different machine-learning strate- gies resulting from different design choices. Figure 2 shows the cumulative performance of the 1,056 long-short portfolios. Each line represents the performance of one specific set of research design choices.
The figure shows that the variation in design choices leads to a substantial variation in returns. A hypothetical $1 investment in 1987 leads to a final wealth ranging from $0.94 (annual compounded return of -0.17%) to $2,652 (annual compounded return of 24.48%) in 2021. The best model is associated with design choices of Algorithm (ENS ML), Target (RET-MKT, RAW), Feature (No Post Publication, No Feature Selection), and Training (Expanding Window, ExMicro Training Sample). On the other hand, the worst-performing model is associated with the design choices of Algorithm (RF), Target (RET-CAPM, RAW), Feature (Yes Post Publication, Yes Feature Selection), and Training (Rolling Window, All Training Sample). The details of the top- and bottom-performing models are documented in Appendix Table B.2. Apart from that, we also observe that all the machine learning models perform worse in recent years, particularly after 2004, which aligns with the findings of Blitz et al. (2023).
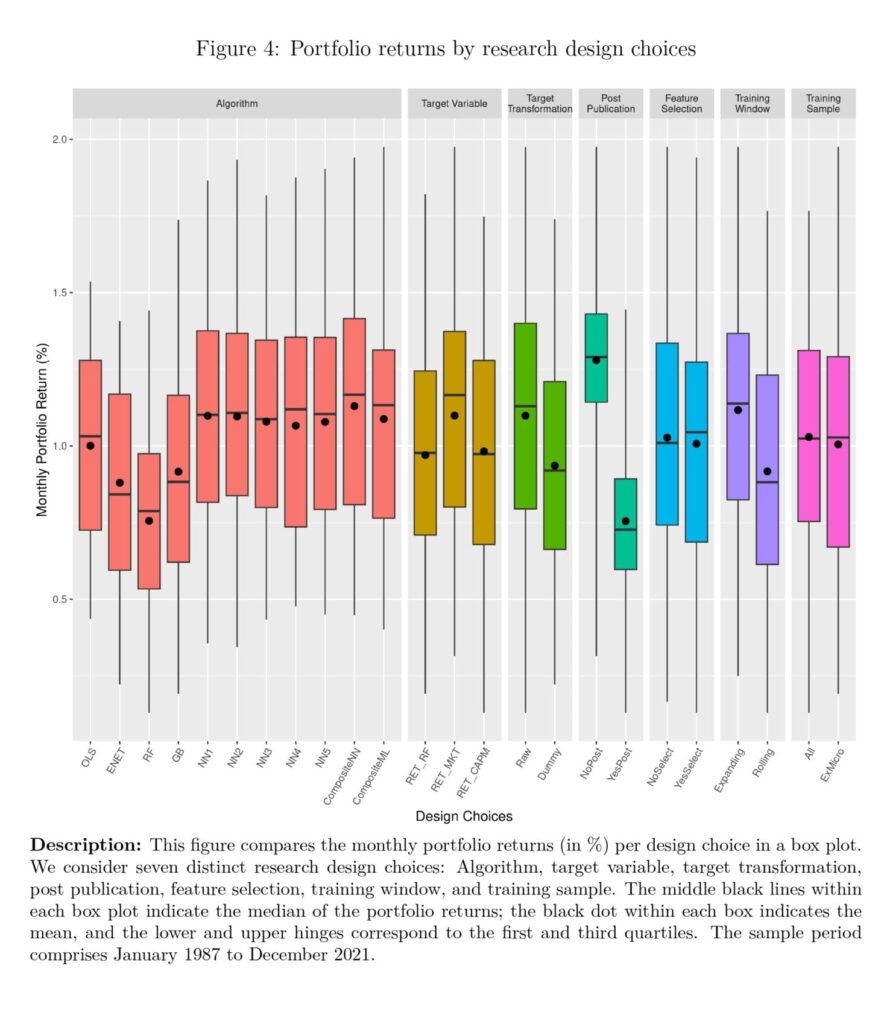
Figure 4 shows the portfolio returns in a box plot with the mean, median, first quartile, third quartile, minimum, and maximum values.
The algorithm choice contains eleven alternatives, comprising linear methods (OLS, ENET), tree-based methods (RF and GB), neural networks with one to five hidden layers (NN1-NN5), as well as an ensemble of all neural networks (ENS NN) and an ensemble of all non-linear ML methods (ENS ML). The results show that the composite methods exhibit higher mean and median portfolio returns than the other nine individual algorithms. While our primary focus is not to compare individual algorithms, we notice that the neural networks (NN) display better performance, whereas random forest (RF), on average, performs the worst.”
Are you looking for more strategies to read about? Sign up for our newsletter or visit our Blog or Screener.
Do you want to learn more about Quantpedia Premium service? Check how Quantpedia works, our mission and Premium pricing offer.
Do you want to learn more about Quantpedia Pro service? Check its description, watch videos, review reporting capabilities and visit our pricing offer.
Are you looking for historical data or backtesting platforms? Check our list of Algo Trading Discounts.
Or follow us on:
Facebook Group, Facebook Page, Twitter, Linkedin, Medium or Youtube
Share onLinkedInTwitterFacebookRefer to a friend