Forecasting the VIX to Improve VIX-Derivatives Trading

A related paper has been added to:

#198 – Exploiting Term Structure of VIX Futures

Authors: Donninger

Title: Forecasting the VIX to Improve VIX-Derivatives Trading

Link: http://papers.ssrn.com/sol3/papers.cfm?abstract_id=2771019

Abstract:

Konstantinidi et. al. state in their broad survey of Volatility-Index forecasting: "The question whether the dynamics of implied volatility indices can be predicted has received little attention". The overall result of this and the quoted papers is: The VIX is too a very limited extend (R2 is typically 0.01) predictable, but the effect is economically not significant. This paper confirms this finding if (and only if) the forecast horizon is limited to one day. But there is no practical need to do so. One can – and usually does – hold a VIX Future or Option several trading days. It is shown that a simple model has a highly significant predictive power over a longer time horizon. The forecasts improve realistic trading strategies.

Notable quotations from the academic research paper:

"Konstantinidi et. al. investigate in [E. Konstantinidi., G. Skiadopoulos, E. Tzagkaraki: Can the Evolution of Implied Volatility be Forecasted? Evidence from European and U.S. Implied Volatility Indices. Draft from 18/12/2007] different models for forecasting several volatility indexes one day ahead. There is no practical need to restrict the forecast to one day. The one day convention is for trading purposes unusual. One either trades intraday or over a longer time horizon. It is well known that the VIX has a mean-reverting behavior. Mean-reversion is swamped in the short run by the high volatility of the index. But it should be possible to exploit mean-reversion in the long run. The best – and most practical – model I have found is:

VIXret(h) = a0 + a1*VIX(t) + a2*VXV(t) + a3*IVTS(t)

VIXret(h) is log(VIX(t+h)) – log(VIX(t)) where h is the forecast horizon in trade days.
VIX(t) is the current VIX-value.
VXV(t) is the 3-months volatility index.
IVTS(t) is the implied-volatility-term-structure defined as VIX(t)/VXV(t).

The model uses the current VIX level, VXV can be interpreted as a smoothed version of the VIX. The IVTS is a measure of the current term-structure.

Campasano & Simon proposed in [J. Campasano, D. Simon: The VIX Futures Basis: Evidence and Trading Strategies. June 27, 2012] a simple VIX Futures strategy to exploit the positive bias.

The daily roll of a VIX-Future is defined as:

R(t) = (VXF(t) – VIX(t))/TTS(t)

VXF is the VIX Futures Price.
TTS are the Trade-days Till Settle (expiry).

One enters a short VIX Future position if R(t) is above a given threshold and sells the Futures back if the basis is either below a lower threshold or one is close to the expiry. One can replace the current VIX value with the VIX forecast at expiry. The strategy with the plain VIX has a P&L of 110.2% with a Sharpe-Ratio of 0.93 and a maximum relative drawdown of 18.2%. The forecast improves this to a P&L of 156.2%, a Sharpe-Ratio of 1.12 and a drawdown of 16.8%.

"

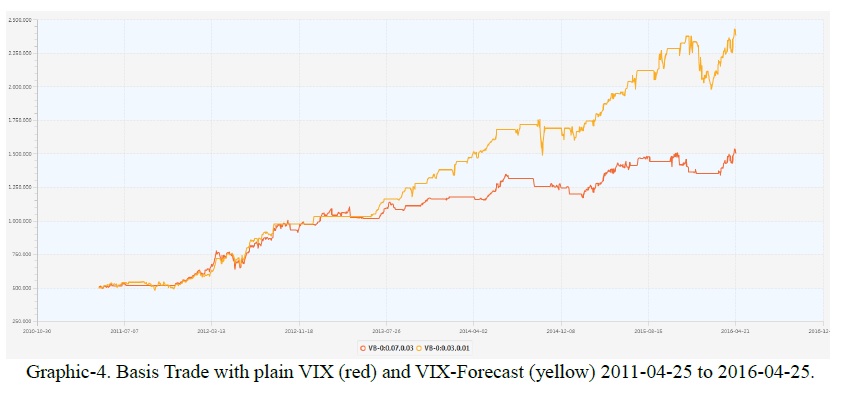Are you looking for more strategies to read about? Sign up for our newsletter or visit our Blog or Screener.

Do you want to learn more about Quantpedia Premium service? Check how Quantpedia works, our mission and Premium pricing offer.

Do you want to learn more about Quantpedia Pro service? Check its description, watch videos, review reporting capabilities and visit our pricing offer.

Are you looking for historical data or backtesting platforms? Check our list of Algo Trading Discounts.

Would you like free access to our services? Then, open an account with Lightspeed and enjoy one year of Quantpedia Premium at no cost.

Or follow us on:

Facebook Group, Facebook Page, Twitter, Linkedin, Medium or Youtube