How Often Should We Rebalance Equity Factor Portfolios?
Quantpedia has already covered a countless number of factor investing strategies and articles, from strategies in our Screener to multiple blog posts. Therefore, we can confidently say that we do like factor investing. However, there is always new research with a unique point of view. For example, we recently found a paper focused on the decay of the factor exposures of quantamental equity factor strategies. The study examines five factors: Value, Momentum, Quality, Investment, and Low Volatility, across 12 developed and emerging markets over a 20-year period. This research aims to find out how long it takes for a factor to decay after the portfolio is assembled. In other words, how often should the portfolio be rebalanced?
First, the authors analyze portfolio factor exposures as random variables of an unknown distribution. Secondly, they attempt to quantify these distributions for a selected group of factor strategies and thus examine the factor’s evolution over time. In addition, the authors introduce a factor half-life metric to describe an optimal rebalancing period by quantifying the rate of decay.
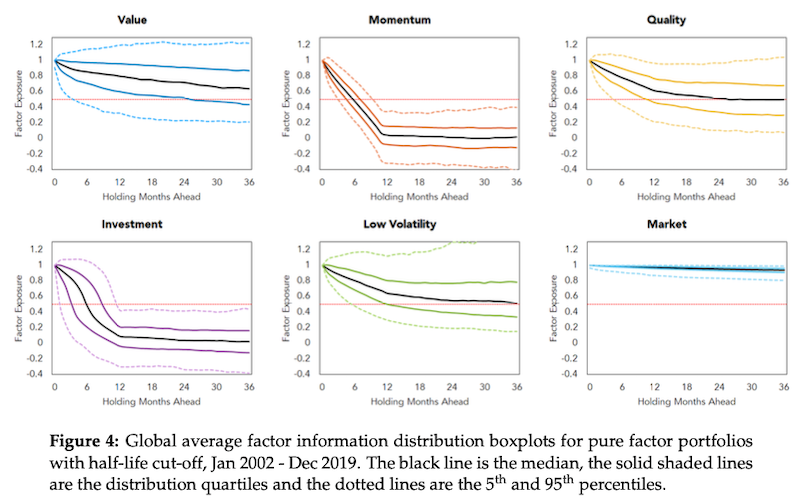
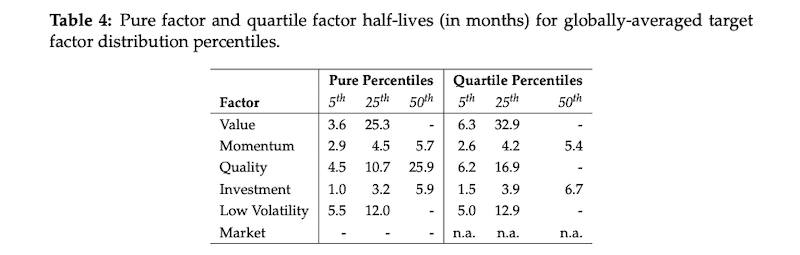
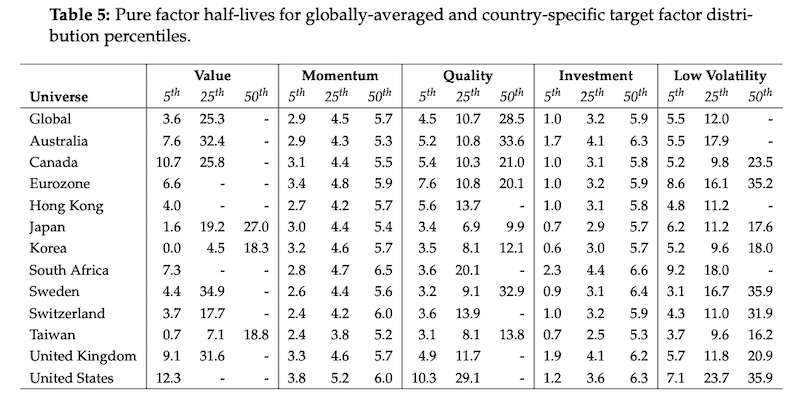
The results of this paper indicate that, of the factors they studied, the fastest decaying ones are Momentum and Investment. In contrast, the slowest decaying factors include Value, followed by Low Volatility and Quality. Additionally, the recommended rebalancing periods vary from 3 months (for Momentum) up to 6 months (for Low Volatility), depending on the factor.
Authors: Emlyn Flint, Rademeyer Vermaak
Title: Factor Information Decay: A Global Study
Link: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3986499
Abstract:
This research addresses a simple but important unanswered question in the factor investing literature: how do the factor exposures of equity factor strategies decay over time? The answer to this question has two important practical consequences. Firstly, understanding how a strategy’s factor exposures change over time informs the optimal rebalancing period. Secondly, when coupled with factor risk premia estimates, it describes the term structure of expected returns per factor strategy. To answer this question, we conduct a large-scale empirical study of five well-known factors – Value, Momentum, Quality, Investment and Low Volatility – across 12 developed and emerging markets over the last 20 years. We calculate factor exposure, or information, distributions per market for both pure and quartile long/short factor portfolios, and then analyse how these distributions decay over a 36-month holding period. In order to formally measure the rate of information decay, we introduce the idea of a factor half-life metric and use the global half-life results to propose optimal rebalancing periods per factor.
As always, we present several interesting figures:
Notable quotations from the academic research paper:
“One particular area that continues to receive considerable attention is the measurement and analysis of portfolio factor exposures over time (e.g. Israel and Ross, 2017; Ang et al., 2017; Blitz and Vidojevic, 2019). This attention is natural given that factor exposures, either directly or indirectly, form the basis of all factor-based portfolio construction and risk management applications.
We add to this body of knowledge by addressing a simple but important unanswered question: how do the factor exposures of common equity factor strategies decay over time?
The natural question that arises then is how will these exposures change in future as one continues to hold the portfolio and as factor information updates? When thought of in this manner, it becomes clear that portfolio factor exposures are in fact random variables, and that the evolution of these variables over time must be described by a certain distribution. The purpose of this study is to quantify these distributions for a select group of factor strategies, and thereafter study their evolution over time. Such a study has two important practical consequences. Firstly, understanding how a strategy’s factor exposures are expected to change over time directly informs the strategy’s optimal rebalancing period. Secondly, when coupled with factor risk premia estimates, it also allows one to fully describe the term structure of expected returns for that strategy.
There are two specific areas in the literature that are closely related to our work, and thus worth highlighting. The first area relates to the handful of studies that seek to define and measure the ’efficiency’ of a factor portfolio. Hunstad and Dekhayser (2015) were arguably the first to formalise this concept through the introduction of their factor efficiency ratio metric, defined as the ratio of active risk coming from the desired (or target) factors to that coming from the undesired (or non-target) factors.1 More recently, Brown et al. (2019) suggest measuring efficiency as the percentage contribution to absolute risk from the desired factors, while Bender and Sun (2019) propose the ratio of a portfolio’s target factor exposure to its tracking error as an alternative metric.
The second area relates to research done in identifying optimal holdings periods. The most well-known of these studies is the seminal paper on Momentum by Jegadeesh and Tit- man (1993) who, among other things, analysed the effect that changing a Momentum portfolio’s formation and holding periods has on average return. Similar formation-versus-holding period analyses for the Momentum factor have since been conducted across multiple time periods and markets. In most cases, the findings remain consistent: average return is maximised for medium-term formation periods and holding periods (3-12 months). Furthermore, a number of these studies show global maxima for the specific combination of a 12-month formation period and a 3-month holding period (e.g. Scowcroft and Sefton, 2005).
Based on the empirical results, we confirm that Value is the slowest decaying factor on average, followed closely by Low Volatility and then Quality. The pure Investment and Momentum factors are then the quickest decaying factors by a considerable margin.
Motivated by the global factor Value-at-Risk half-life results, we propose rebalance periods for each pure factor. In particular, we propose that the information-optimal rebalance period is 3 − 4 months for Value, 3 months for Momentum, 4 − 5 months for Quality, 1 month for Investment, and 5 − 6 months for Low Volatility.
Finally, we discuss the link between pure factor exposure distributions and portfolio expected return and propose that, under the assumption of constant factor risk premia, the global and country-specific factor half-life results presented here can also be used as reason- able approximations for the expected return half-lives of each pure factor portfolio.”
Are you looking for more strategies to read about? Sign up for our newsletter or visit our Blog or Screener.
Do you want to learn more about Quantpedia Premium service? Check how Quantpedia works, our mission and Premium pricing offer.
Do you want to learn more about Quantpedia Pro service? Check its description, watch videos, review reporting capabilities and visit our pricing offer.
Are you looking for historical data or backtesting platforms? Check our list of Algo Trading Discounts.
Or follow us on:
Facebook Group, Facebook Page, Twitter, Linkedin, Medium or Youtube
Share onLinkedInTwitterFacebookRefer to a friend