What is Bitcoin’s Fair Value ?
Nice academic paper uses Metcalfe’s law to estimate Bitcoin's fundamental value. A really recommended read … :
Authors: Wheatley, Sornette, Huber, Reppen, Gantner
Title: Are Bitcoin Bubbles Predictable? Combining a Generalized Metcalfe's Law and the LPPLS Model
Link: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3141050
Abstract:
We develop a strong diagnostic for bubbles and crashes in bitcoin, by analyzing the coincidence (and its absence) of fundamental and technical indicators. Using a generalized Metcalfe’s law based on network properties, a fundamental value is quantified and shown to be heavily exceeded, on at least four occasions, by bubbles that grow and burst. In these bubbles, we detect a universal super-exponential unsustainable growth. We model this universal pattern with the Log-Periodic Power Law Singularity (LPPLS) model, which parsimoniously captures diverse positive feedback phenomena, such as herding and imitation. The LPPLS model is shown to provide an ex-ante warning of market instabilities, quantifying a high crash hazard and probabilistic bracket of the crash time consistent with the actual corrections; although, as always, the precise time and trigger (which straw breaks the camel’s back) being exogenous and unpredictable. Looking forward, our analysis identifies a substantial but not unprecedented overvaluation in the price of bitcoin, suggesting many months of volatile sideways bitcoin prices ahead (from the time of writing, March 2018).
Notable quotations from the academic research paper:
"The explosive growth of bitcoin intensified debates about the cryptocurrency’s intrinsic or fundamental value. While many pundits have claimed that bitcoin is a scam and its value will eventually fall to zero, others believe that further enormous growth and adoption await, often comparing to the market capitalization of monetary assets, or stores of value. By comparing bitcoin to gold, an analogy that is based on the digital scarcity that is built into the bitcoin protocol, some markets analysts predicted bitcoin prices as a high as 10 million per bitcoin.
There is an emerging academic literature on cryptocurrency valuations and their growth mechanisms. Many of these studies attribute some technical feature of the bitcoin protocol, such as the “proof-of-work” system on which the bitcoin cryptocurrency is based, as a source of value. However, as has been proposed by former Wall Street analyst Tom Lee, an early academic proposal, by now widely discussed within cryptocurrency communities, is that an alternative valuation of bitcoin can be based on its network of users. In the 1980s, Metcalfe proposed that the value of a network is proportional to the square of the number of nodes. This may also be called the network effect, and has been found to hold for many networked systems. If Metcalfe’s law holds here, fundamental valuation of bitcoin may in fact be far easier than valuation of equities—which relies on various multiples, such as price-to-earnings, price-to-book, or price-to-cash-flow ratios—and will therefore admit an indication of bubbles.
Here, we combine—as a fundamental measure—a generalized Metcalfe’s law and—as a technical measure—the LPPLS model, in order to diagnose bubbles in bitcoin. When both measures coincide, this provides a convincing indication of a bubble and impending correction. If, in hindsight, such signals are followed by a correction similar to that suggested, they provide compelling evidence that a bubble and crash did indeed take place.
Given the number of active users, and calibrations of the generalized Metcalfe’s law, which maps to market cap, we can now compare the predicted market cap with the true one, as in Figure 2. Also, using smoothed active users, the local endogeneities—where price drives active users—are assumed to be averaged out. The OLS estimated regression, by definition, fits the conditional mean, as is apparent in Figure 2. Therefore, if bitcoin has evolved based on fundamental user growth with transient overvaluations on top, then the OLS estimate will give an estimate in-between and thus above the fundamental value. For this reason, support lines are also given, and—although their parameters are chosen visually—they may give a sounder indication of fundamental value. In any case, the predicted values for the market cap indicate a current over-valuation of at least four times. In particular, the OLS fit with parameters (1.51,1.69), the support line with (0,1.75), and the Metcalfe support line (-3,2) suggest current values around 44, 22, and 33 billion USD, respectively, in contrast to the actual current market cap of 170 billion USD. Further, assuming continued user growth in line with the regression of active users starting in 2012, the end of 2018 Metcalfe predictions for the market cap are 77, 39, and 64 billion USD respectively, which is still less than half of the current market cap. These results are found to be robust with regards to the chosen fitting window.
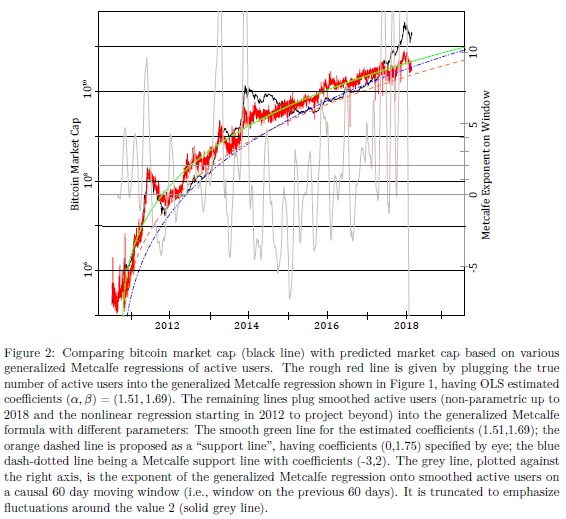
"
Are you looking for more strategies to read about? Check http://quantpedia.com/Screener
Do you want to see performance of trading systems we described? Check http://quantpedia.com/Chart/Performance
Do you want to know more about us? Check http://quantpedia.com/Home/About
Follow us on:
Facebook: https://www.facebook.com/quantpedia/
Twitter: https://twitter.com/quantpedia