The Importance of Factor Construction Choices
Choosing the correct portfolio-construction techniques is very important. The new paper that is written by Amar Soebhag, Bart van Vliet, and Patrick Verwijmeren explores the various ways in which different design choices in portfolio construction can, either intentionally or unintentionally, influence and distort the statistical results of a market factor’s research. Their takeaway is that seemingly small differences in design can significantly impact the resultant portfolio’s performance.
On a sample of stocks listed on NYSE, AMEX, and NASDAQ with share codes 10 or 11, the authors study how the factor construction impacts its returns. They study the impact of characteristic breakpoints (30th and 70th/20th and 80th percentile, with the latter resulting in more extreme characteristics chosen into the portfolio), breakpoints universe (NYSE/NYSE-AMEX-NASDAQ, but again, AMEX and NASDAQ are tilted toward smaller stocks, resulting in a tilt toward these in the portfolio), microcaps (included/excluded), financial firms(included/excluded), industry hedging (because some factors might be present on an unconditional sample, but disappear in industry-hedged portfolios), weighting (equally-weighted/value-weighted), time of observation of the market capitalization (June of a given year/every month), and dependent/independent sorting (when using an independent sort, some portfolios may remain empty, which is solved by a dependent sort, but then the question of the sorting order arises). To sum it up, there are two possibilities for 8 portfolio construction choices, resulting in 256 possible construction alternatives considered.
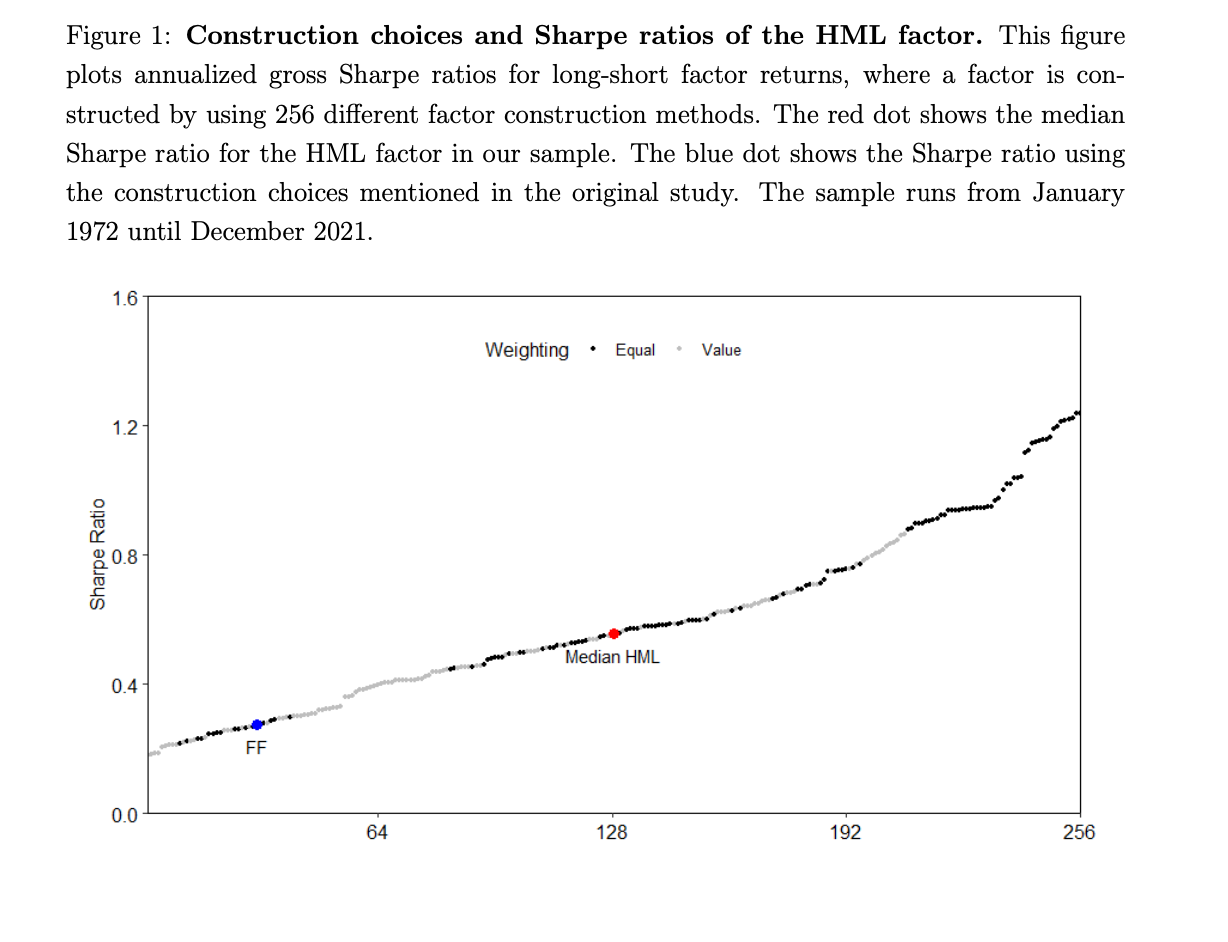
As you can see below, in the Figure 1 of the paper, when using equal-weighted portfolio construction, gross returns and Sharpe ratios tend to be higher. Quite intuitively, also using 20th and 80th percentile breakpoints, a breakpoint univese consisting of NYSE-AMEX-NASDAQ, including microcaps and financial firms result in higher Sharpe ratio. However, even though for example equal-weighted portfolio has higher Sharpe ratio, it doesn’t have higher net returns because of the high transaction costs. Including microcaps, NYSE-AMEX-NASDAQ breakpoints or ignoring industry-adjustments leads to a similiar result of better gross return, but worse net return.
Authors: Amar Soebhag, Bart van Vliet, and Patrick Verwijmeren
Title: Non-Standard Errors in Asset Pricing: Mind Your Sorts?
Link: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=4136672
Abstract:
Researchers face a number of design choices when constructing factors to study asset returns. We examine to which extent these construction choices matter. By purposely data mining over 250 different versions of each factor, we find that Sharpe ratios exhibit substantial variation within a factor due to different construction choices, which results in sizable non-standard errors and allows for p-hacking. Our study has important implications for model selection exercises.
Notable quotations from the academic research paper:
“Interestingly, researchers face a number of choices when constructing factors and the choices being made vary substantially across studies. These differential choices lead to non-standard errors (Menkveld et al., 2021): in addition to a data-generating process, there is an evidence-generating process that leads to uncertainty due to variation in research design choices.
A better understanding of the design choices that matter allows researchers to more effectively show the robustness of their findings in future work, while also helping readers in interpreting the presented results. Understanding the non-standard errors in asset pricing is also important because researchers have incentives to engage in p-hacking (Harvey, 2017): ambiguity regarding construction choices creates room for researchers to construct factors in a way that maximizes some statistical criteria, such as maximizing Sharpe ratios and t-statistics.
The non-standard errors in our setting can be defined as the standard deviation of the generated Sharpe ratios across the possible construction methods. We find that non-standard errors are sizable relative to standard errors, across all factors. In multiple cases, the non-standard errors exceed the standard errors.
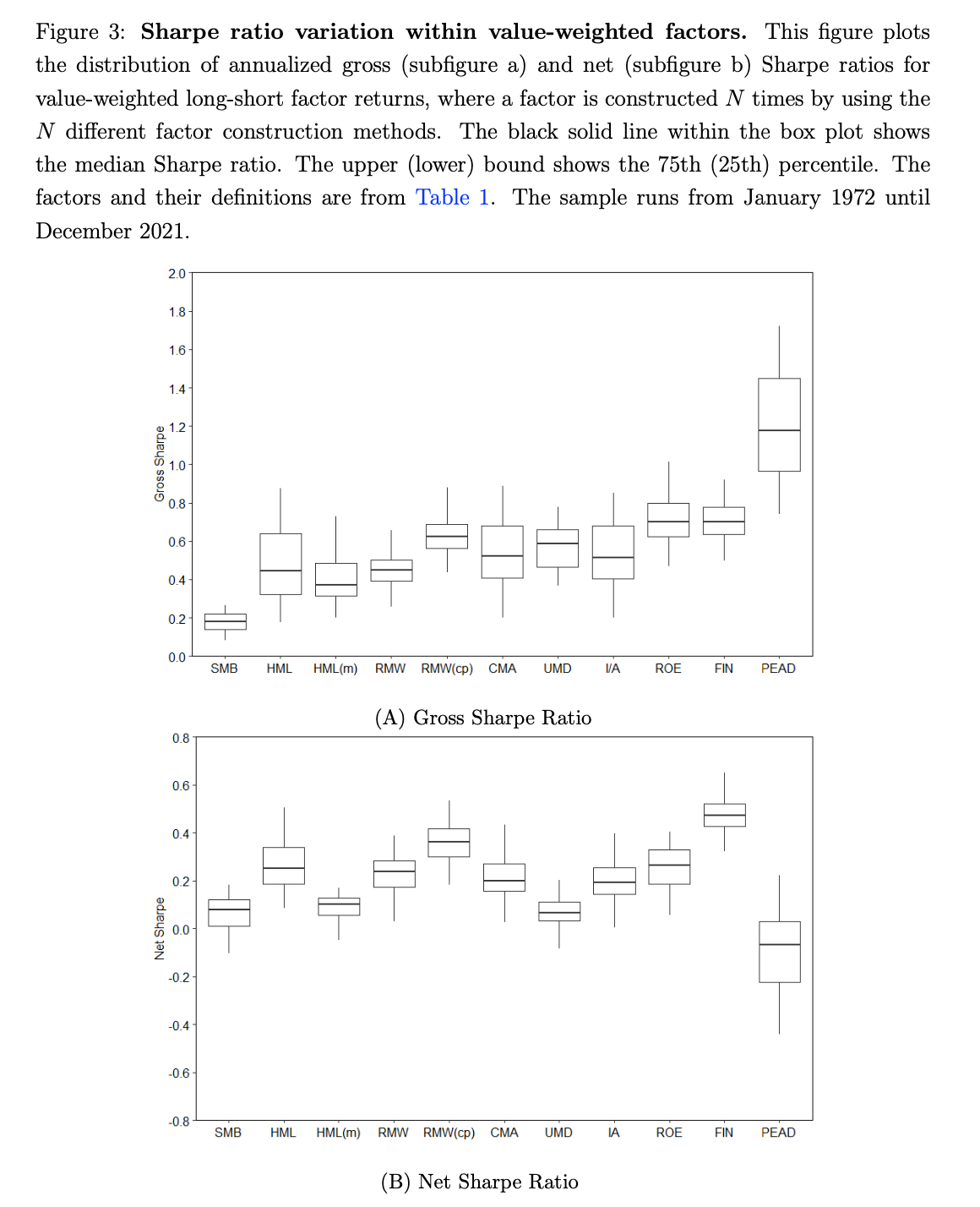
Using NAN breakpoints instead of NYSE breakpoints improves gross Sharpe ratios from 0.54 to 0.74, which is the largest increase within our set of choices. On a net basis, the difference is much smaller. By using NAN-breakpoints, we allow more small caps to enter the portfolio construction, which have larger transaction costs. Including microcaps improve the gross Sharpe ratio from 0.59 to 0.70. However, on a net basis, we find that including microcaps yields a Sharpe ratio of 0.07, whereas excluding microcaps results in a Sharpe ratio of 0.17.
Including financial firms increases the gross Sharpe ratio, on average, from 0.63 to 0.66. Our previous results show that the size depth is not significantly altered when we include financial firms, but it does allow for more factor breadth and thus allows to make spread portfolios with a larger differences in the sorting characteristic. It can further be seen that eliminating industry exposures from factor returns increases gross Sharpe ratios, which is in line with Daniel et al. (2020).
Equal-weighing portfolios improves the gross Sharpe ratio compared to value-weighting portfolios from 0.58 to 0.71, on average. However, equal-weighted factor portfolios are tilted towards small caps with higher transaction costs. Hence, the performance on a net-of-cost basis is lower than for value-weighted factor portfolios.
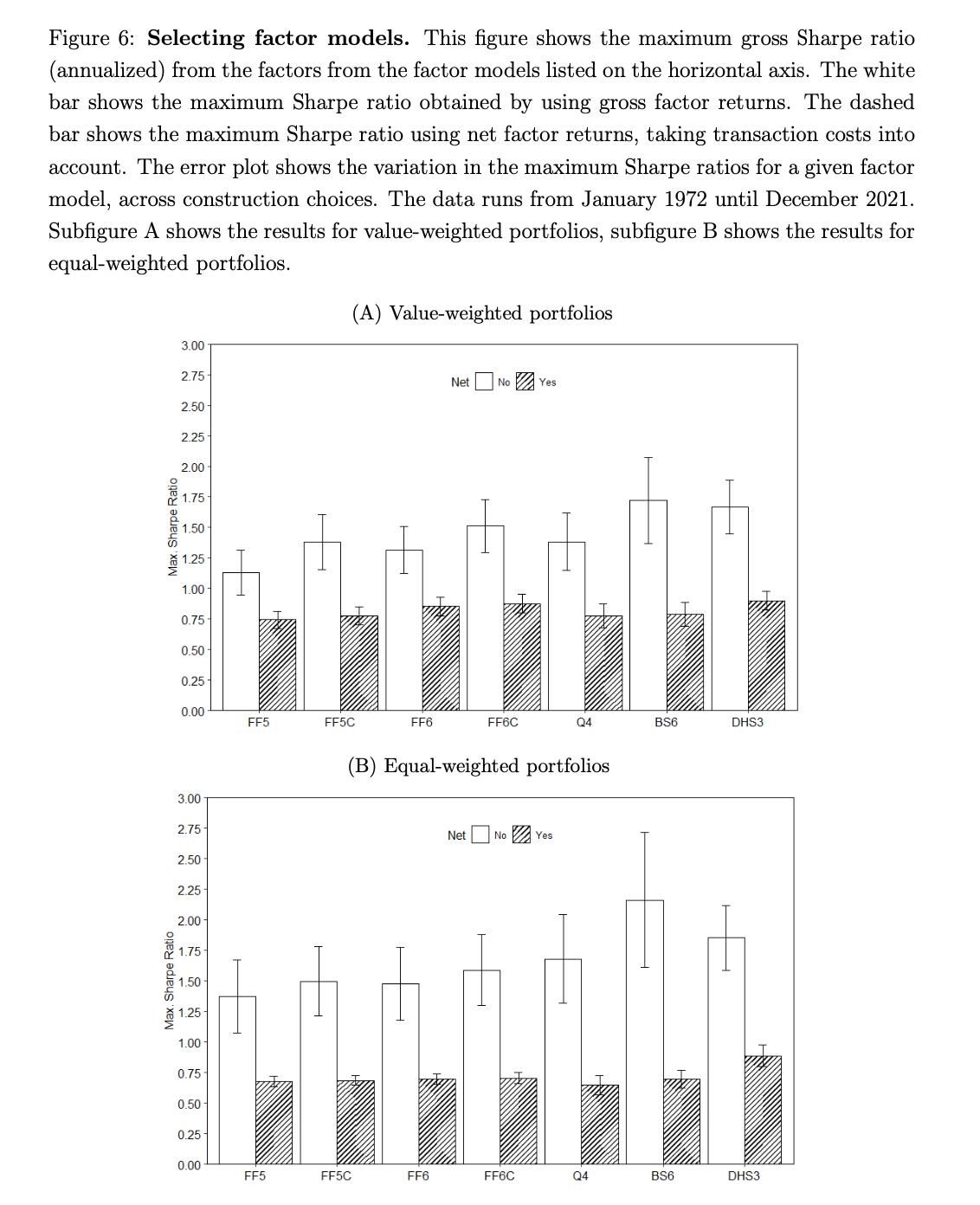
Our approach is based on comparing factor models using the same construction choices, and then averaging over the set of available choices. If a researcher would choose different construction methods for different factor models, there would be a possibility that model rankings differ, and these possibilities are represented by the error bars in the figure.
Panel B of Figure 6 shows the model selection results when we equal weight factor returns. Compared to the value-weighted results, average gross Sharpe ratios increase, but the same applies to the standard deviations.
In addition to an impact on factor exposure, construction choices may impact the liquidity of a portfolio. Stocks with low liquidity, such as microcaps, may have high transaction costs and other frictions (such as bid-ask spreads), which could directly impact the returns of factor portfolios.
Factor portfolios with few stocks may have a higher variance term, resulting into under-diversification and lower risk-adjusted return. For example, if we use 20th-80th breakpoints instead of 30th-70th breakpoints, we select fewer stocks into the factor portfolio, thereby introducing more idiosyncratic or unpriced risk. In addition, selecting stocks that are highly correlated increases the second term, especially when the portfolio consists of a few stocks. Another example is that unhedged factors may tilt towards certain industries, resulting in a selection of stocks with potentially higher correlations. Choosing to hedge out industry exposure will reduce correlations among assets, decreasing the second term.”
Are you looking for more strategies to read about? Sign up for our newsletter or visit our Blog or Screener.
Do you want to learn more about Quantpedia Premium service? Check how Quantpedia works, our mission and Premium pricing offer.
Do you want to learn more about Quantpedia Pro service? Check its description, watch videos, review reporting capabilities and visit our pricing offer.
Or follow us on:
Facebook Group, Facebook Page, Twitter, Linkedin, Medium or Youtube
Share onLinkedInTwitterFacebookRefer to a friend