Quantopian & Quantpedia Trading Strategy Series: Reversals in the PEAD
Our sucessful Quantopian & Quantpedia Trading Strategy Series continues with a third article, written by Matthew Lee, focused on Reversal During Post-Earnings Announcement Drift (Strategy #238):
https://www.quantopian.com/posts/quantpedia-trading-strategy-series-reversals-in-the-pead
(Click on a "View Notebook" button to read a complete analysis)
What is the logic behind this strategy? Jonathan A. Milian in his paper "Overreacting to a History of Underreaction" explores the possibility that well known cross sectional anomalies can reverse over time. And he picks the premier anomaly – Post Earnings Announcement Drift. He finds that stocks with the most negative previous earnings surprise actually exhibit the most positive returns very shortly after the subsequent earnings announcement.
The academic paper speculates that it seems that due to well-documented history of investors underreacting to earnings news, investors are now overreacting to earnings announcement news. Investors position themselves in alignment with the expectation of the PEAD effect so when the next earnings announcement comes, the overcrowding of investors pushes the market beyond efficient, resulting in the correction of investor sentiment and a negative correlation for firm's earnings news in the following days. However classical PEAD (post-earnings announcement drift) literature examines mainly quarterly portfolio returns while this academic paper focuses on 2-days retun therefore it is probable that PEAD still holds and both anomalies exists concurrently.
Matthew Lee from Quantopian performed an independed analysis of initial findings of Jonathan A. Milian's original academic paper (over a sample period from 2011 – 2016 compared to the Milian's 2003 – 2010). What Matthew found? Overall, he found his results to be consistent with Milian's results for all strategy's holding periods from 2-10 days. The best result was a hold period of 9 or 10 days following the Earnings Announcement, rather than 2 days. Firms in the highest decile of past earnings surprise underperform stocks in the lowest decile by -1.78% over a hold period of 10 days (compared to -1.59% over a hold period of 3 days found in the paper).
So, what is the trading algorithm?
1. Each day, pick stocks in the S&P500 which have Earnings Announcements the next day
2. Go short on stocks in the highest decile of previous earnings surprise, long on stocks in the lowest decile of previous earnings surprise
3. Hold for a period of 10 days, then close the position
As always, the final OOS equity curve looks really good:
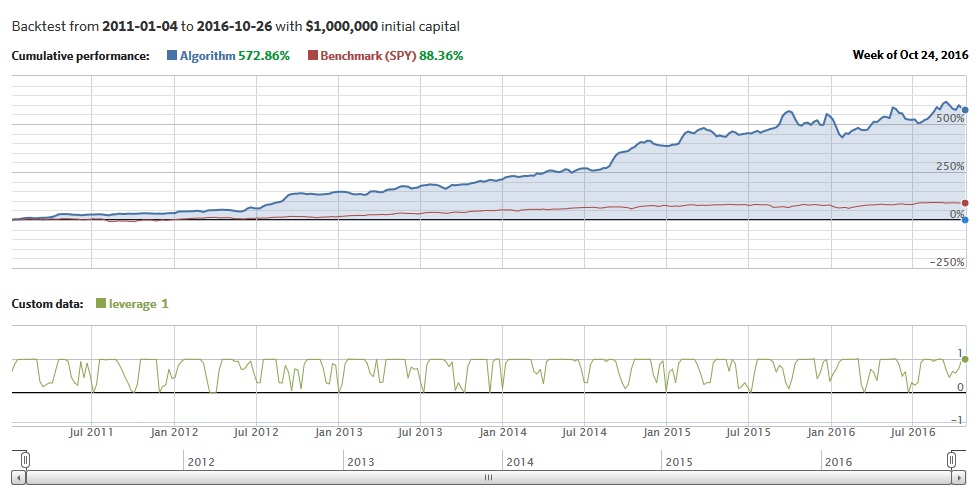
Nice work Matthew!
You may also check first or second article in this series if you liked the current one. And stay tuned for the next …








